Type I and Type II Errors and Statistical Power
Type I and Type II Errors and Statistical Power
Definition/Introduction
Healthcare professionals, when determining the impact of patient interventions in clinical studies or research endeavors that provide evidence for clinical practice, must distinguish well-designed studies with valid results from studies with research design or statistical flaws. This topic helps providers determine the likelihood of type I or type II errors and judge the adequacy of statistical power (see Table. Type I and Type II Errors and Statistical Power). Then, one can decide whether or not the evidence provided should be implemented in practice or used to guide future studies.
Issues of Concern
Register For Free And Read The Full Article
Search engine and full access to all medical articles
10 free questions in your specialty
Free CME/CE Activities
Free daily question in your email
Save favorite articles to your dashboard
Emails offering discounts
Learn more about a Subscription to StatPearls Point-of-Care
Issues of Concern
Understanding the concepts discussed in this topic allows healthcare providers to accurately and thoroughly assess the results and validity of medical research. Without understanding type I and II errors and power analysis, clinicians could make poor clinical decisions without evidence to support them.
Type I and Type II Errors
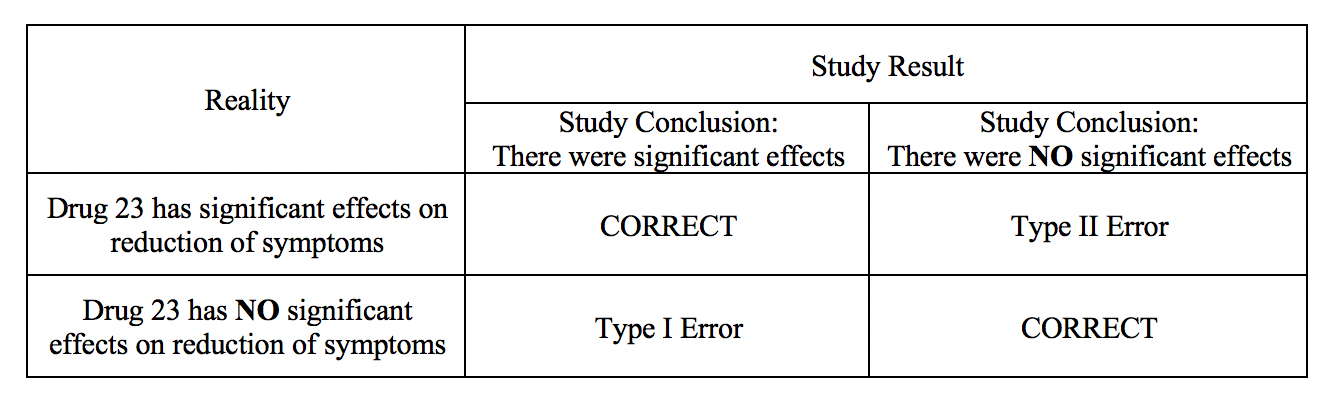
Type I and Type II errors can lead to confusion as providers assess medical literature. A vignette that illustrates the errors is The Boy Who Cried Wolf. First, the citizens commit a type I error by believing there is a wolf when there is not. Second, the citizens commit a type II error by believing there is no wolf when there is one. A type I error occurs when, in research, we reject the null hypothesis and erroneously state that the study found significant differences when there was no difference. In other words, it is equivalent to saying that the groups or variables differ when, in fact, they do not or have false positives.[1]
Here is a sample research hypothesis: Drug 23 will significantly reduce symptoms associated with Disease A compared to Drug 22. If we were to state that Drug 23 significantly reduced symptoms of Disease A compared to Drug 22 when it did not, this would be a type I error. Committing a type I error can be very grave in specific scenarios. For example, if we did move ahead with Drug 23 based on our research findings, even though there was no difference between groups, and the drug costs significantly more money for patients or has more side effects, then we would raise healthcare costs, cause iatrogenic harm, and not improve clinical outcomes. If a p-value is used to examine type I error, the lower the p-value, the lower the likelihood of the type I error to occur.
A type II error occurs when we declare no differences or associations between study groups when, in fact, there were.[2] As with type I errors, type II errors in certain cause problems. Picture an example with a new, less invasive surgical technique developed and tested compared to the more invasive standard care. Researchers would seek to show no differences between patients receiving the 2 treatment methods in health outcomes (noninferiority study). If, however, the less invasive procedure resulted in less favorable health outcomes, it would be a severe error. Table 1 provides a depiction of type I and type II errors. (See Type I and Type II Errors and Statistical Power Table 1)
Power
A concept closely aligned to type II error is statistical power. Statistical power is a crucial part of the research process that is most valuable in the design and planning phases of studies, though it requires assessment when interpreting results. Power is the ability to reject a null hypothesis that is indeed false correctly.[3] Unfortunately, many studies lack sufficient power and should be presented as having inconclusive findings.[4] Power is the probability of a study to make correct decisions or detect an effect when one exists.[3][5]
The power of a statistical test depends on the significance level set by the researcher, the sample size, and the effect size or the extent to which the groups differ based on treatment.[3] Statistical power is critical for healthcare providers to decide how many patients to enroll in clinical studies.[4] Power is strongly associated with sample size; when the sample size is large, power is generally not an issue.[6] Thus, when conducting a study with a low sample size and, ultimately, low power, researchers should be aware of the likelihood of a type II error. The greater the N within a study, the more likely a researcher will reject the null hypothesis. The concern with this approach is that a very large sample could show a statistically significant finding due to the ability to detect small differences in the dataset; thus, using p values alone based on a large sample can be troublesome.
It is essential to recognize that power can be deemed adequate with a smaller sample if the effect size is large.[6] What is an acceptable level of power? Many researchers agree that a power of 80% or higher is credible enough to determine the effects of research studies.[3] Ultimately, studies with lower power find fewer true effects than studies with higher power; thus, clinicians should be aware of the likelihood of a power issue resulting in a type II error.[7] Unfortunately, many researchers and providers who assess medical literature do not scrutinize power analyses. Studies with low power may inhibit future work as they cannot detect actual effects with variables; this could lead to potential impacts remaining undiscovered or noted as ineffective when they may be.[7]
Medical researchers should invest time conducting power analyses to distinguish a difference or association sufficiently.[3] Luckily, there are many tables of power values and statistical software packages that can help determine study power and guide researchers in study design and analysis. If choosing statistical software to calculate power, the following are necessary for entry: the predetermined alpha level, proposed sample size, and effect size the investigator(s) aims to detect.[2] By utilizing power calculations on the front end, researchers can determine an adequate sample size to compute effect and determine, based on statistical findings, that sufficient power was observed.[2]
Clinical Significance
By limiting type I and type II errors, healthcare providers can ensure patients' decisions based on research outputs are safe.[8] Additionally, while power analysis can be time-consuming, making inferences on low-powered studies can be inaccurate and irresponsible. By utilizing adequately designed studies, balancing the likelihood of type I and type II errors, and understanding power, providers, and researchers can determine which studies are clinically significant and should be implemented into practice.
Nursing, Allied Health, and Interprofessional Team Interventions
All physicians, nurses, pharmacists, and other healthcare professionals should strive to understand the concepts of Type I and II errors and power. These individuals should maintain the ability to review and incorporate new literature for evidence-based and safe care. They also more effectively work in teams with other professionals.
Media
(Click Image to Enlarge)
References
Lieberman MD, Cunningham WA. Type I and Type II error concerns in fMRI research: re-balancing the scale. Social cognitive and affective neuroscience. 2009 Dec:4(4):423-8. doi: 10.1093/scan/nsp052. Epub 2009 Dec 24 [PubMed PMID: 20035017]
Singh G. A shift from significance test to hypothesis test through power analysis in medical research. Journal of postgraduate medicine. 2006 Apr-Jun:52(2):148-50 [PubMed PMID: 16679686]
Bezeau S, Graves R. Statistical power and effect sizes of clinical neuropsychology research. Journal of clinical and experimental neuropsychology. 2001 Jun:23(3):399-406 [PubMed PMID: 11419453]
Keen HI, Pile K, Hill CL. The prevalence of underpowered randomized clinical trials in rheumatology. The Journal of rheumatology. 2005 Nov:32(11):2083-8 [PubMed PMID: 16265683]
Level 1 (high-level) evidenceGaskin CJ, Happell B. Power, effects, confidence, and significance: an investigation of statistical practices in nursing research. International journal of nursing studies. 2014 May:51(5):795-806. doi: 10.1016/j.ijnurstu.2013.09.014. Epub 2013 Oct 9 [PubMed PMID: 24207028]
Algina J, Olejnik S. Conducting power analyses for ANOVA and ANCOVA in between-subjects designs. Evaluation & the health professions. 2003 Sep:26(3):288-314 [PubMed PMID: 12971201]
Ueki C, Sakaguchi G. Importance of Awareness of Type II Error. The Annals of thoracic surgery. 2018 Jan:105(1):333. doi: 10.1016/j.athoracsur.2017.03.062. Epub [PubMed PMID: 29233341]
Leon AC. Multiplicity-adjusted sample size requirements: a strategy to maintain statistical power with Bonferroni adjustments. The Journal of clinical psychiatry. 2004 Nov:65(11):1511-4 [PubMed PMID: 15554764]